AI 科技评论按，随着 AI 系统在现实生活中变得越来越重要，我们自然该探索不同系统间的交互方式了，这些多智能体间到底用了什么独特的方式呢?

在 DeepMind 的最新论文(发表在 Scientific Reports ， Nature 出版社旗下杂志)中，研究人员用了博弈论来阐明这一问题。了解到，具体来说，他们研究了两套智能系统在非对称博弈游戏(asymmetric game)中的反应和表现，这些游戏包括 Leduc 扑克和一些图版游戏(如 Scotland Yard)。

在现实生活中，我们会遇到许多类似非对称博弈游戏的场景，自动拍卖(automated auction)就是其中之一。在这一过程中，会混入许多 AI 扮演的买家或卖家，而真正参与其中的人类买家和卖家也都有自己的小算盘。最终的测试结果让研究人员对这种奇怪的情况有了深刻了解，他们还拿出了一个相当简单的分析方法。

虽然 DeepMind 的主要目标是如何将博弈论应用到多个 AI 系统的交互中去，但研究人员得出的结果也可以用在经济、生物进化和实证博弈论等学科中。

众所周知，博弈论是数学界的重量级理论，研究人员通常会用它来研究竞争态势下决策者们的战略，该理论几乎可通用于人类、动物和计算机世界。不过，在 AI 研究中，它一般会被用在“多智能体”环境下的研究中。举例来说，多款家政机器人合作清洁房间就属于其中的应用场景之一。

一般来说，多智能体系统的演化动力学都靠简单的对称博弈论来分析，比如经典的囚徒困境理论。虽然此类游戏能帮我们对多智能体系统的工作方式有一定了解，并告诉我们如何实现你好我好大家好的理想结果(即所谓的纳什均衡)，但却无法模拟所有情况。

DeepMind 的新技术让研究人员能快速容易地在更复杂的不对称博弈游戏中找到取得纳什均衡的策略，这类游戏中玩家通常有不同的战略、目标和奖励。如果你想了解 DeepMind 是如何用新技术“破解”这类游戏的，可以试着去了解“性别博弈”，它也是博弈论研究的经典案例之一。

在“性别博弈”中，两个玩家要协调晚上到底去哪玩，是去看歌剧还是看电影?令人遗憾的是，他们中有一个人倾向于看歌剧，另一个人则偏爱电影。这样的情境下，不对称的情况就出现了，因为即使两个人达成一致，其中也有一个人会不高兴。因此，要想继续维持两人的友谊(划掉)，或者说均衡，玩家就该共进退(毕竟产生分歧换来的只有零回报)。

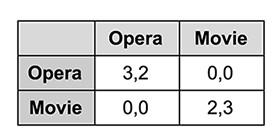
这个游戏有三种“势均力敌”的均衡情况

第三种选项是一种“不稳定”(unstable)选项，用 DeepMind 的方法很轻松就能进行简化或者分解，非对称博弈游戏也就转换成为对称的对应部分。这一方法将两个玩家的奖励表分别当作独立的双玩家对称博弈，这样也能轻松地找到原本不对称博弈游戏的纳什均衡点。

在下图中，b 和 c 图的纳什均衡点很容易找到，借助它们我们就能在非对称博弈中找到 a 图中的最佳策略。当然，我们也可以反过来，通过非对称博弈来找寻对应体中的平衡点。

两个玩家都决定去看歌剧，

两人都选择去看电影，

则是混合选项，即每位玩家在夜晚外出的五分之三时间内享用自己的心头好。

红点代表纳什均衡。对于非对称博弈游戏(a)，可以从(b)与(c)代表的两个对应图中找到纳什均衡。如图所示，x轴和y轴分别代表玩家1和2选择看歌剧的可能性。

这种方法还可运用于其他游戏，比如 Leduc 扑克，在论文中研究人员还对它进行了详细解读。无论哪种情况下，这种方法都足够简单，它能帮玩家快速和直接的分析非对称博弈游戏，进而帮助我们理解不同的动态系统，其中就包括多主题环境下的系统交互。